Flow instabilities past permeable bluff bodies
A classical and pertinent subject within fluid mechanics is the interaction between fluid flows and bluff bodies. The von Kármán vortex street, named after the Hungarian-American physicist Theodore von Kármán, is a phenomen characterized by the formation of alternating vortices that trail behind the object invested by a stream. These vortices are known to create alternate loads on slender objects, eventually leading to catastrophic events. Nature consistently offers inspiring models when it comes to shaping objects so as to serve practical purposes. Deep-sea glass (E. aspergillum) are tall, holed, cylindrical shells anchored to the seabed that extend through the benthic boundary layer. These sponges provide a natural shelter for a family of shrimps which feed themselves through the nutrients in suspension thanks to the internal recirculation patterns at low flow velocity of such permeable structures. Dandelion seeds are transported by the wind attached to a hairy umbrella structure, called pappus, which helps the seed to travel for large distances. These examples show how permeable structures offer an efficient way to maximize, without the need for active control systems, the hydrodynamic performance and eventually stabilize unsteady patterns. In the video below, we show the wake developing past an array of wires in a water channel, visualized through hydrogen bubbles.
Flow past an array of wires visualized through hydrogen bubbles.
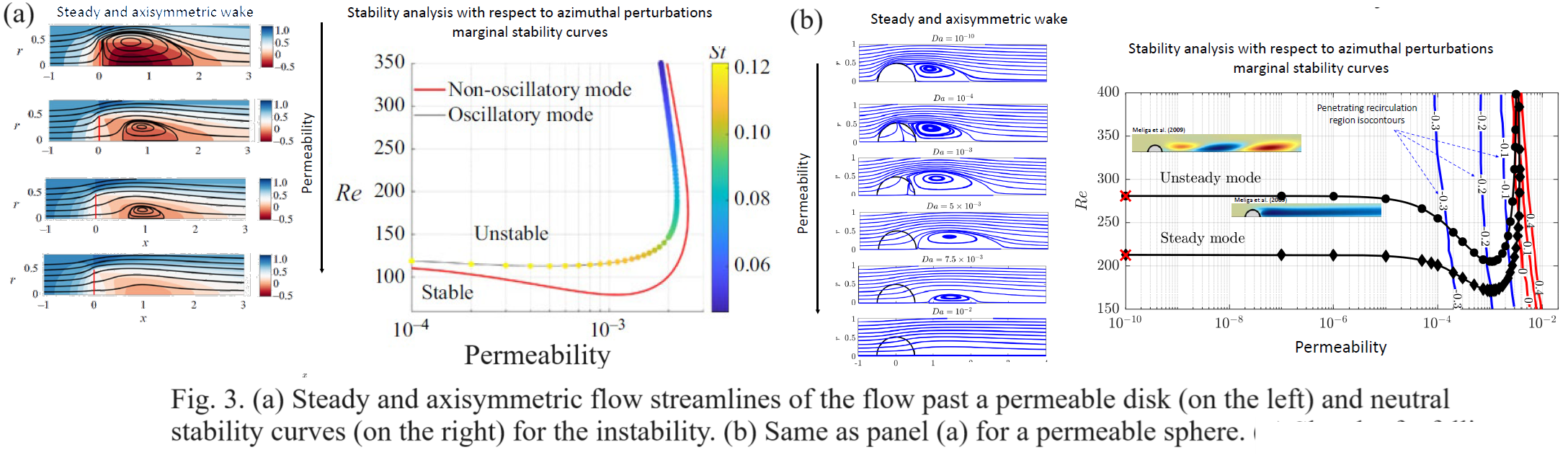
As initial benchmark aimed at unveiling the formation of vortex streets around slender permeable bodies at low Reynolds numbers, we examine a permeable cylinders of various sections subjected to a uniform flow. The porous body's internal flow follows a Darcy-Brinkman model, while the incompressible Navier-Stokes equations govern the external flow. In the case of steady flow past these objects, a detached recirculation bubble emerges, progressing downstream, diminishing in size and eventually disappearing with increasing permeability. Nevertheless, a velocity defect persists past the object for greater downstream distances when compared to the impervious scenario. The modifications of the wake in the onset of unsteady flow are studied through a linear stability analysis approach. The increase of permeability in slender cylinders results in a sudden increase in the critical Reynolds number for the onset of the von Karman vortex street. Beyond a critical value, the onset of the unsteady wake is suppressed. Similarly, the unsteady 2D wake structure is explored in the unsteady regime, revealing that alternate vortices endure at considerably larger distances, in contrast to the impervious case. The threshold for the onset of the three-dimensional instability in such unsteady periodic flow is also identified using a Dynamic-Mode-Decomposition-based stability algorithm.
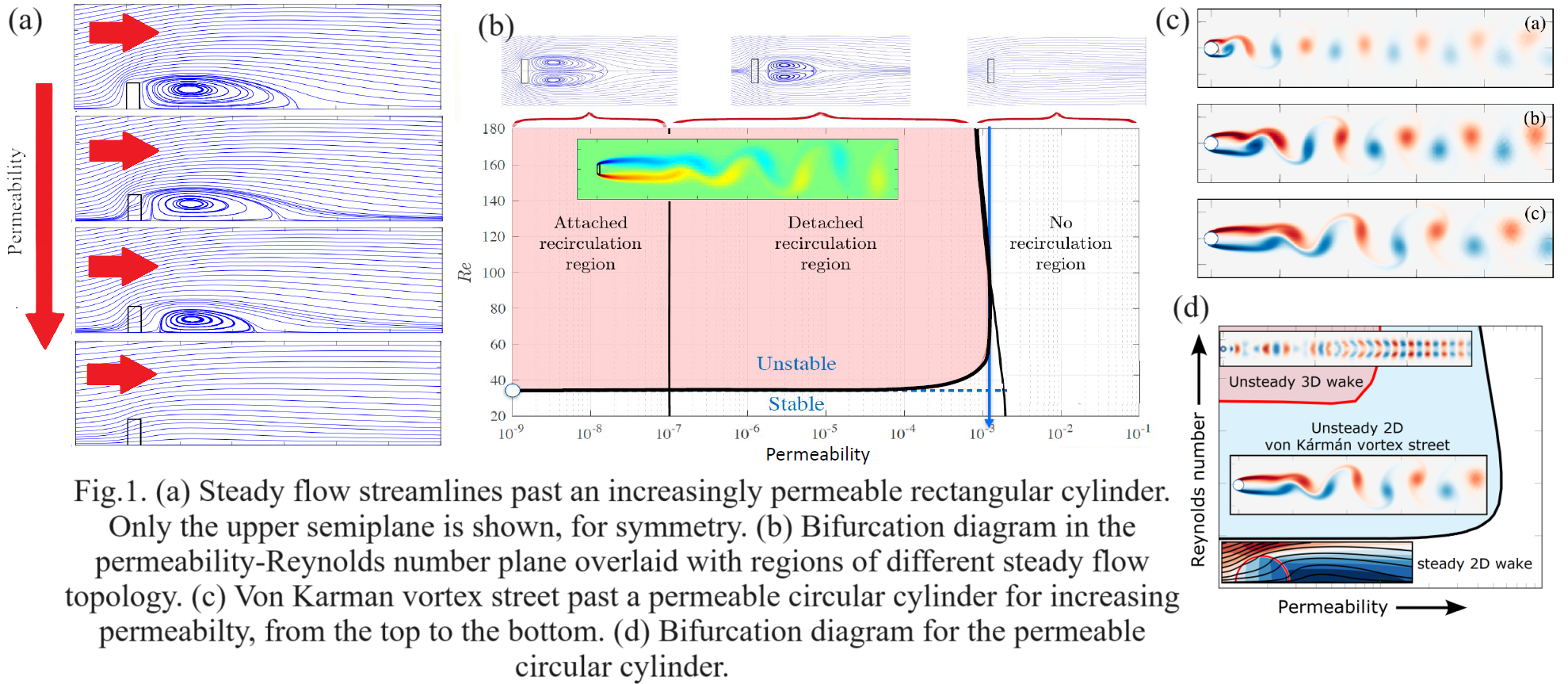
Once the flow picture past slender permeable objects is established, we tailor the structure of our porous body to optimize hydrodynamic performance. To achieve this, we propose a formal framework for characterizing and optimizing the flow around permeable membranes through homogenization. This framework is applied to the two-dimensional wake flow past a permeable cylindrical shell. Homogenization establishes a connection between permeable filtration laws and the full-scale structure. An effective stress jump condition is employed to model the presence of the membrane, with normal and tangential velocities at the membrane proportional to the permeability and slip coefficient, respectively. A procedure for obtaining the microscopic geometry is implemented and validated for uniform distributions of permeability and slip over the membrane. Variations in filtrability and slip along the membrane are then considered, and their distributions are optimized to meet a specified objective using adjoint-based optimization. The optimal distributions are subsequently linked back to the microscopic geometry through a homogenization-based inverse procedure.
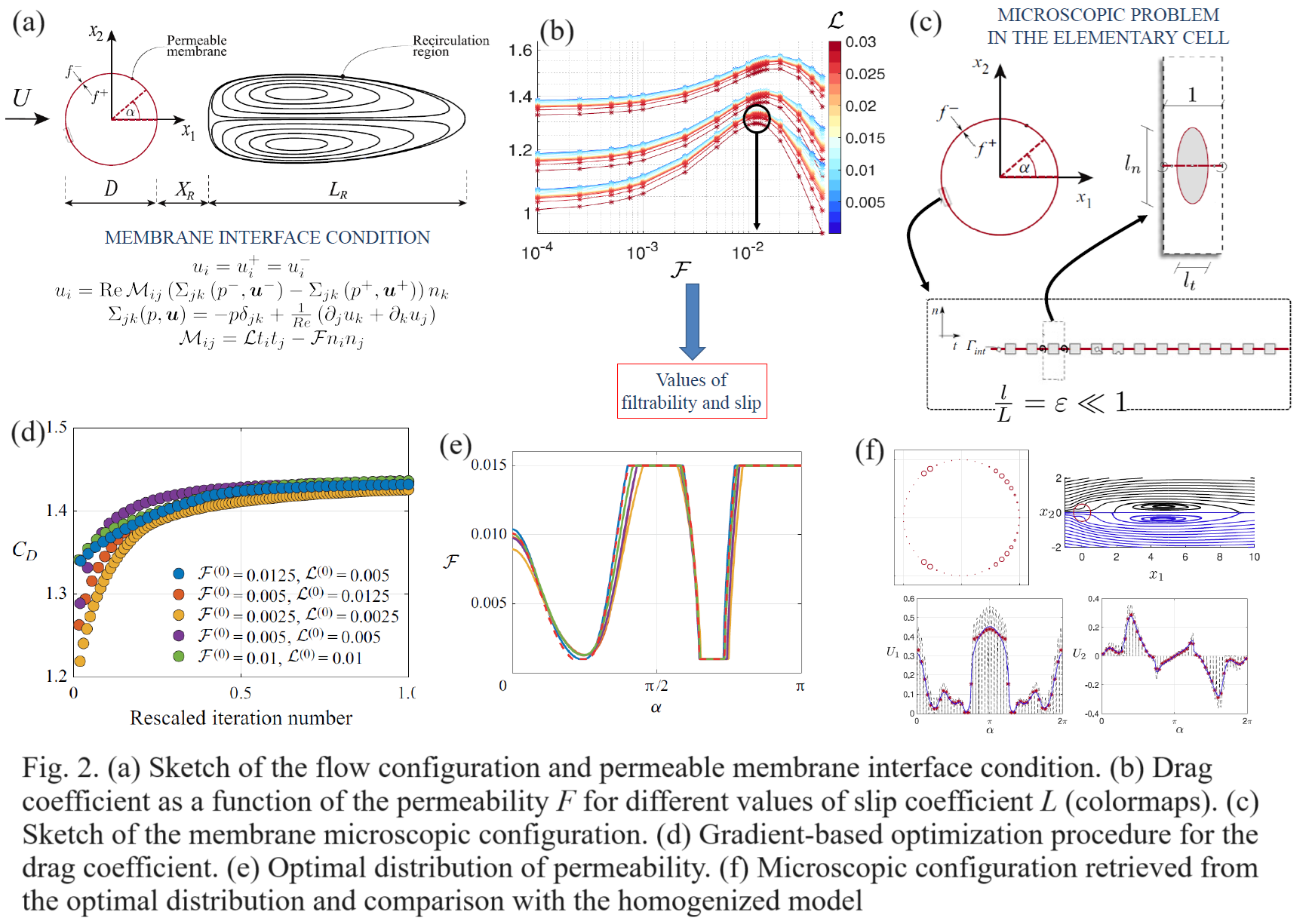
Similar increases in instability thresholds are observed for fixed disks and spheres, although, counter-intuitively, the sphere exhibits a range of permeability where the critical Reynolds number decreases. These findings could pave the way for a rational design of permeable structures to exploit aerodynamic and hydrodynamic flows.